Funciones explícitas e implícitas
Una función es explícita si viene dada como y = f(x) , es decir, la variable dependiente y está despejada.
Una función es implícita si viene dada de la forma f(x, y) = 0 , es decir, si la función se expone como una expresión algebraica igualada a 0.
Toda función expresada en forma explícita se puede poner en forma implícita y viceversa.
Ejemplos
1) La función y = 7x – 3 está expresada en forma explícita y la podemos transformar en implícita haciendo las transformaciones algebraicas adecuadas.
La función y – 7x + 3 = 0 estaría expresada en forma implícita.
2) La función y + 3x2 – 8x + 5 = 0 está expresada en forma implícita y si despejamos la variable y obtenemos la forma explícita.
Es decir, y = – 3x2 + 8x – 5 sería la forma explícita
Funciones uniformes y relaciones multiformes
Si a cada valor de la variable independiente le corresponde un solo valor de la imagen ƒ(X), se dice que la función es uniforme.
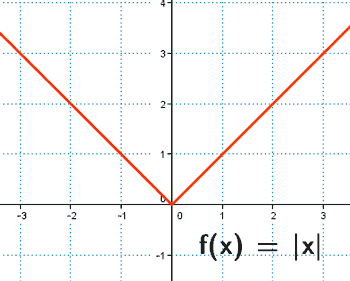
Si le corresponden dos o más valores no se trata de una función sino de una relación o fórmula llamada comúnmente multiforme.